publications

2025

1. 

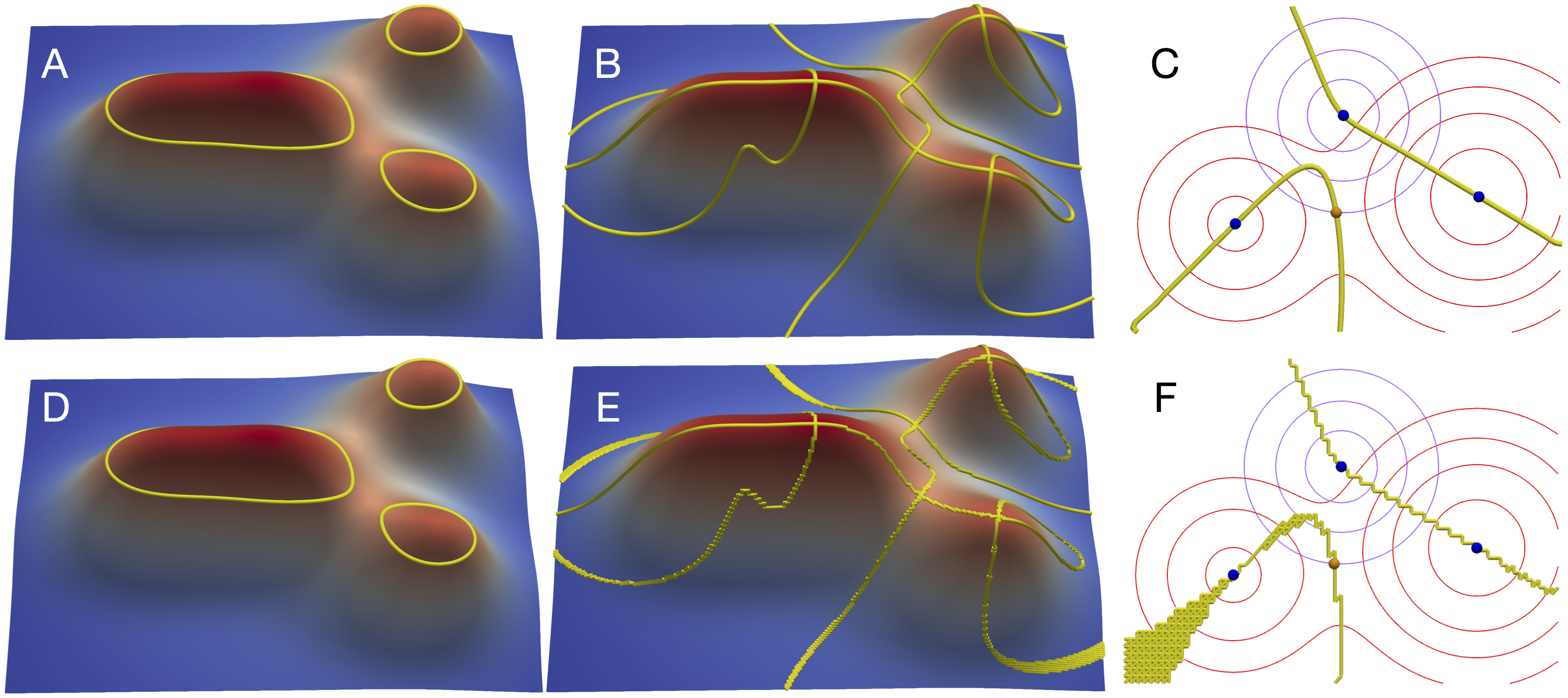   Extracting Complex Topology from Multivariate Functional Approximation: Contours, Jacobi Sets, and Ridge-Valley Graphs

   Guanqun Ma, David Lenz, Hanqi Guo, and 2 more authors

   In 2025 Large Data Analysis and Visualization (LDAV), 2025

   Abs PDF

   Implicit continuous models, such as functional models and implicit neural networks, are an increasingly popular method for replacing discrete data representations with continuous, high-order, and differentiable surrogates. These models offer new perspectives on the storage, transfer, and analysis of scientific data. In this paper, we introduce the first framework to directly extract complex topological features – contours, Jacobi sets, and ridge-valley graphs – from a type of continuous implicit model known as multivariate functional approximation (MFA). MFA replaces discrete data with continuous piecewise smooth functions. Given an MFA model as the input, our approach enables direct extraction of complex topological features from the model, without reverting to a discrete representation of the model. Our work is easily generalizable to any continuous implicit model that supports the queries of function values and high-order derivatives. Our work establishes the building blocks for performing topological data analysis and visualization on implicit continuous models.

2. 

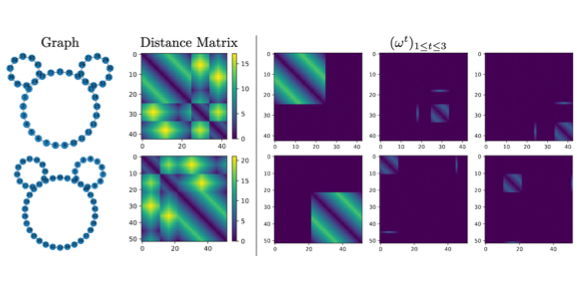   Metrics for Parametric Families of Networks

   Mario Gómez, Guanqun Ma, Tom Needham, and 1 more author

   Under Review, 2025

   Abs PDF

   We introduce a general framework for analyzing data modeled as parameterized families of networks. Building on a Gromov-Wasserstein variant of optimal transport, we define a family of parameterized Gromov-Wasserstein distances for comparing such parametric data, including time-varying metric spaces induced by collective motion, temporally evolving weighted social networks, and random graph models. We establish foundational properties of these distances, showing that they subsume several existing metrics in the literature, and derive theoretical approximation guarantees. In particular, we develop computationally tractable lower bounds and relate them to graph statistics commonly used in random graph theory. Furthermore, we prove that our distances can be consistently approximated in random graph and random metric space settings via empirical estimates from generative models. Finally, we demonstrate the practical utility of our framework through a series of numerical experiments.

2024

1. 

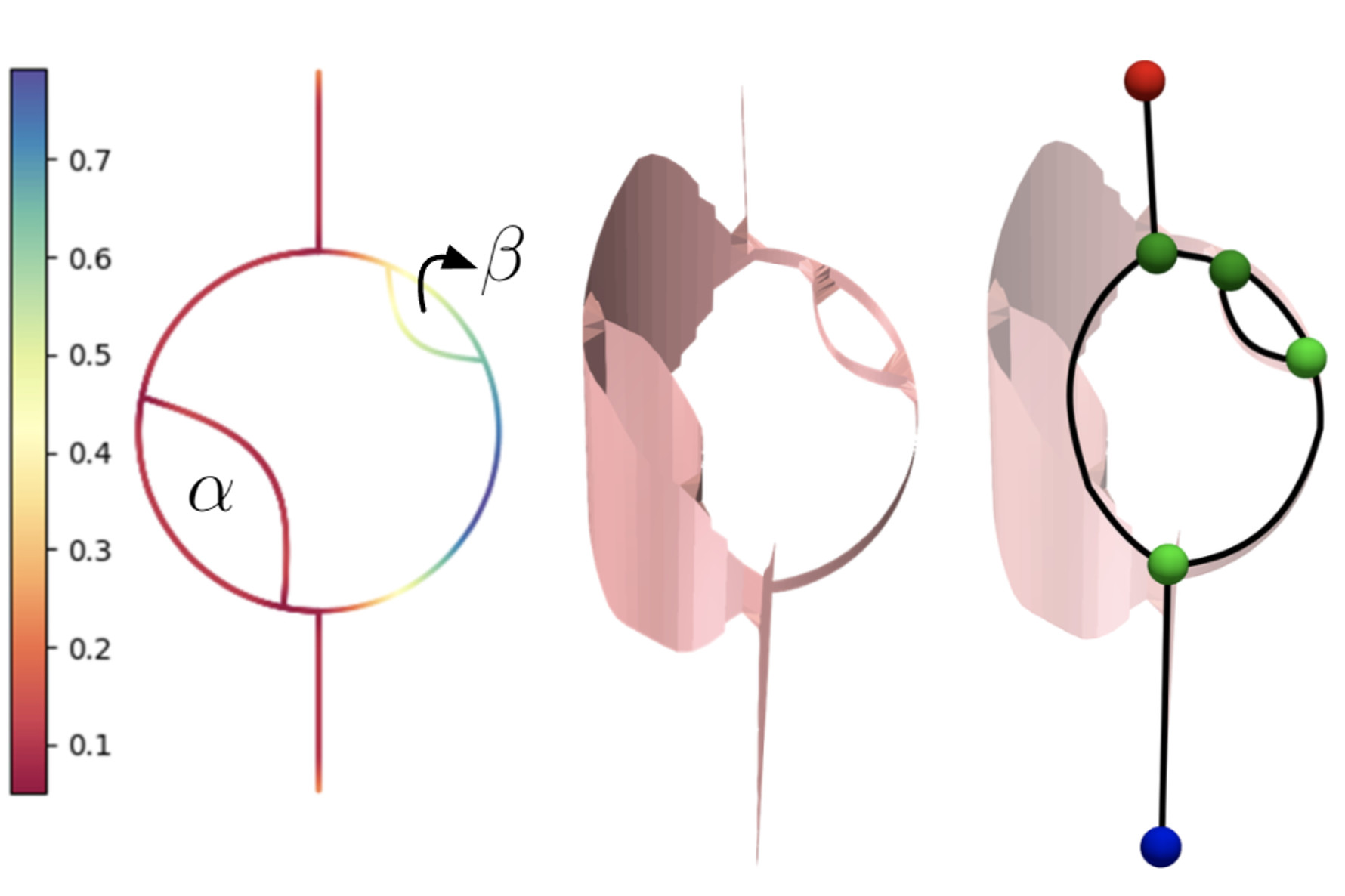   Measure-Theoretic Reeb Graphs and Reeb Spaces

   Qingsong Wang, Guanqun Ma, Raghavendra Sridharamurthy, and 1 more author

   In 40th International Symposium on Computational Geometry (SoCG 2024), 2024

   Abs PDF

   A Reeb graph is a graphical representation of a scalar function on a topological space that encodes the topology of the level sets. A Reeb space is a generalization of the Reeb graph to a multiparameter function. In this paper, we propose novel constructions of Reeb graphs and Reeb spaces that incorporate the use of a measure. Specifically, we introduce measure-theoretic Reeb graphs and Reeb spaces when the domain or the range is modeled as a metric measure space (i.e., a metric space equipped with a measure). Our main goal is to enhance the robustness of the Reeb graph and Reeb space in representing the topological features of a scalar field while accounting for the distribution of the measure. We first introduce a Reeb graph with local smoothing and prove its stability with respect to the interleaving distance. We then prove the stability of a Reeb graph of a metric measure space with respect to the measure, defined using the distance to a measure or the kernel distance to a measure, respectively.

2. 

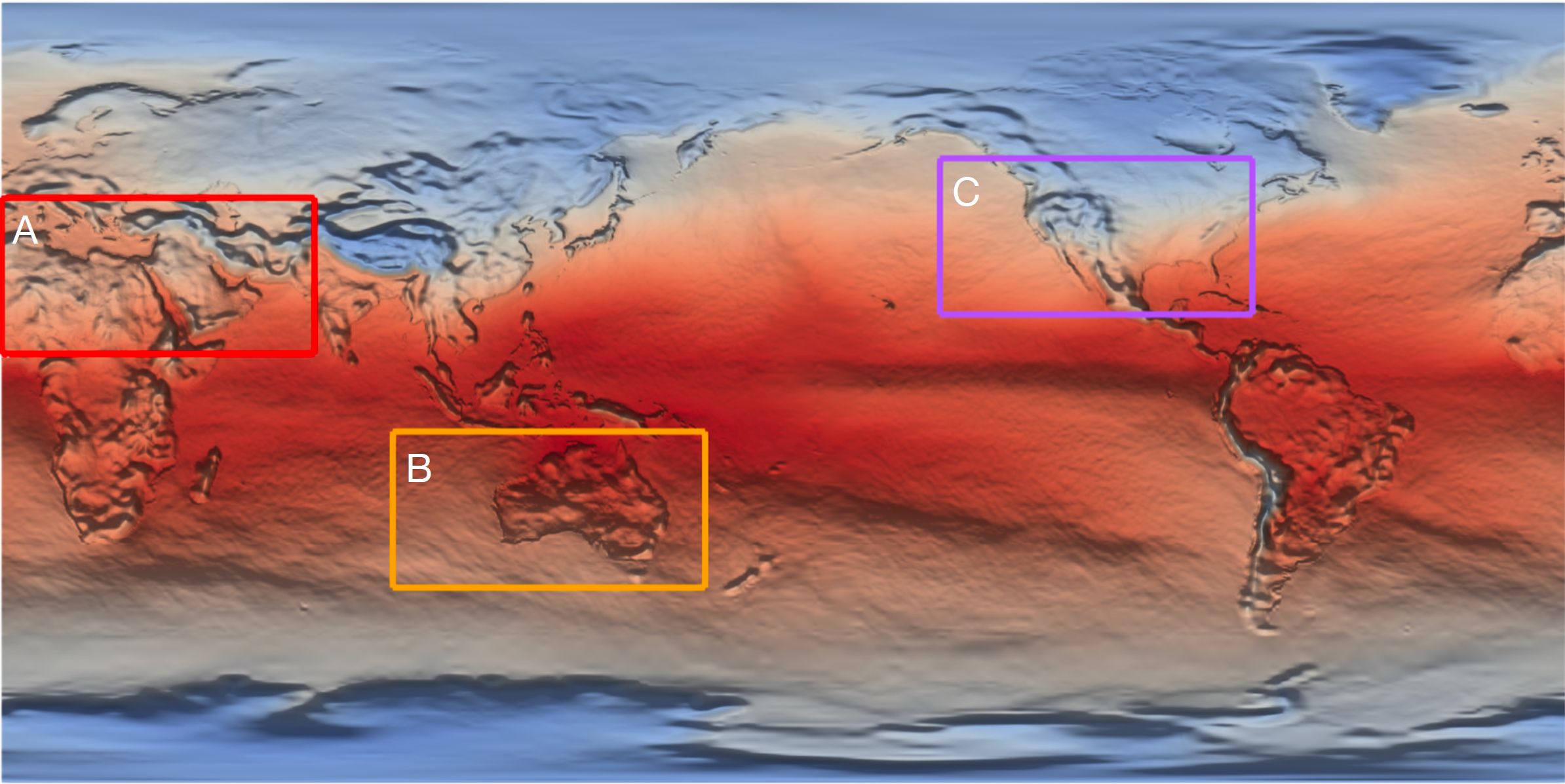   Critical Point Extraction from Multivariate Functional Approximation

   Guanqun Ma, David Lenz, Tom Peterka, and 2 more authors

   In 2024 Topological Data Analysis and Visualization (TopoInVis), 2024

   Abs PDF

   Advances in high-performance computing require new ways to represent large-scale scientific data to support data storage, data transfers, and data analysis within scientific workflows. Multivariate functional approximation (MFA) has recently emerged as a new continuous meshless representation that approximates raw discrete data with a set of piecewise smooth functions. An MFA model of data thus offers a compact representation and supports high-order evaluation of values and derivatives anywhere in the domain. In this paper, we present CPE-MFA, the first critical point extraction framework designed for MFA models of large-scale, high-dimensional data. CPE-MFA extracts critical points directly from an MFA model without the need for discretization or resampling. This is the first step toward enabling continuous implicit models such as MFA to support topological data analysis at scale.

2022

1. 

   Penetration-free projective dynamics on the GPU

   Lei Lan, Guanqun Ma, Yin Yang, and 3 more authors

   In ACM Transa. Graph. (SIGGRAPH), Jul 2022

   Abs PDF

   We present a GPU algorithm for deformable simulation. Our method offers good computational efficiency and penetration-free guarantee at the same time, which are not common with existing techniques. The main idea is an algorithmic integration of projective dynamics (PD) and incremental potential contact (IPC). PD is a position-based simulation framework, favored for its robust convergence and convenient implementation. We show that PD can be employed to handle the variational optimization with the interior point method e.g., IPC. While conceptually straightforward, this requires a dedicated rework over the collision resolution and the iteration modality to avoid incorrect collision projection with improved numerical convergence. IPC exploits a barrier-based formulation, which yields an infinitely large penalty when the constraint is on the verge of being violated. This mechanism guarantees intersection-free trajectories of deformable bodies during the simulation, as long as they are apart at the rest configuration. On the downside, IPC brings a large amount of nonlinearity to the system, making PD slower to converge. To mitigate this issue, we propose a novel GPU algorithm named A-Jacobi for faster linear solve at the global step of PD. A-Jacobi is based on Jacobi iteration, but it better harvests the computation capacity on modern GPUs by lumping several Jacobi steps into a single iteration. In addition, we also re-design the CCD root finding procedure by using a new minimum-gradient Newton algorithm. Those saved time budgets allow more iterations to accommodate stiff IPC barriers so that the result is both realistic and collision-free. Putting together, our algorithm simulates complicated models of both solids and shells on the GPU at an interactive rate or even in real time.

2019

1. Local Low-Rank and Sparse Representation for Hyperspectral Image Denoising

   Guanqun Ma, Ting-Zhu Huang, Jie Huang, and 1 more author

   IEEE Access, Jul 2019

   Abs PDF

   Hyperspectral image (HSI) denoising is a fundamental task in a plethora of HSI applications. Global low-rank property is widely adopted to exploit the spectral-spatial information of HSIs, providing satisfactory denoising results. In this paper, instead of adopting the global low-rank property, we propose to adopt a local low rankness for HSI denoising. We develop an HSI denoising method via local low-rank and sparse representation, under an alternative minimization framework. In addition, the weighted nuclear norm is used to enhance the sparsity on singular values. The experiments on widely used hyperspectral datasets demonstrate that the proposed method outperforms several state-of-the-art methods visually and quantitatively.